| 发电机废气处理 |
| 发动机排气噪声 |
| 发电机风机噪声 |
| 机房的隔声吸声 |
| 排烟系统消音 |
| 排送风系统消音 |
| 空调内部噪声治理 |
| 风机气流噪声治理 |
| 空调末端噪声治理 |
| 空调风管噪声治理 |
| 空调机房噪声治理 |
| 落水装置噪声治理 |
| 冷却塔隔声屏 |
| 冷却塔消声器 |
| 冷却塔消声窗 |
| 低频振动噪音治理 |
| 电梯摩擦噪音治理 |
| 机房噪音的隔声 |
| 电梯井的隔声 |
| 水泵房隔音降噪 |
| 钢铁企业噪音治理 |
| 纺织厂噪音治理 |
| 工厂车间降噪处理 |
| 工业空压机噪声 |
| 机械设备噪声治理 |
| 配电房噪声治理 |
| 水泥厂噪音治理 |
| 民用建筑降噪工程 |
| 酒吧KTV噪声治理 |

l 在均匀的理想流体媒质中的小振幅声波的波动方程是:
![]() ,其中:c——声速,t——时间
,其中:c——声速,t——时间
由上述方程得出:①声波的传递是三维立体,全空间传递的。
②声波的传递受时间、媒质、温度、声压、波长、频率影响。
③具有各向同性的声波传递,理论上可以定向描述,既可以二维平面,或是一维/单向描述。
l 如根据波面形状(时间、媒质、波长因素)分析可定义平面声波、球面声波、柱面声波。
平面声波:当波阵面是垂直于传播方向的一系列平面时的声波。一般远离声源的声波近似的看作为平面声波。如:管道中的活塞往复运动时,在管内同一截面上各质点将同时受到压缩或扩张,具有相同的振幅和相位,这就是平面声波。如果管道始端的活塞以正(余)弦函数的规律往复运动,则称为简谐振动。
在均匀理想流体媒质中,小振幅平面声波的波动方程为:
![]() (均匀理想流质媒质中:无能量耗损)
(均匀理想流质媒质中:无能量耗损)
如果观察在某一确定时刻![]() 时声波在空间沿各方向分布的情况,其波形如图(a)所示。如果要观察在空间定点位置
时声波在空间沿各方向分布的情况,其波形如图(a)所示。如果要观察在空间定点位置![]() 处声波随时间的变化情况,其波形如图(b)所示:
处声波随时间的变化情况,其波形如图(b)所示:
![]()

![]()
![]() (如上例中的活塞偏离平衡位置的距离)
(如上例中的活塞偏离平衡位置的距离)
![]()
![]()
![]()
![]() :声速是声音或者说是声波振幅的传播速度,也是声能量的传递速度。
:声速是声音或者说是声波振幅的传播速度,也是声能量的传递速度。
而声阻抗![]() 中的
中的![]() 指媒介质点的上下振动速度(
指媒介质点的上下振动速度(![]() )。(P10)
)。(P10)
式中:![]() 称为质点振动的速度振幅,单位:帕(斯卡)秒每米(Paּs/m)。
称为质点振动的速度振幅,单位:帕(斯卡)秒每米(Paּs/m)。
球面声波:在各向同性的均匀媒质中,从一个表面同步涨缩的点声源发出的声波,也就是在以声源点为球心,以任何r值为半径的球面上声波的相位相同。
其波动方程为:(r为球半径)
![]()
柱面声波:波阵面是同轴圆柱面的声波,其声源一般可视为“线声源”。简单的柱面声波声场与坐标系的角度和轴向长度无关,仅与径向半径r相关。
![]()
对于远场简谐柱面声波有:
![]() ,可见,随径向距离增加,声压振幅减少,且与距离平方根成反比。
,可见,随径向距离增加,声压振幅减少,且与距离平方根成反比。
上述介绍均为理想状态,实际中可视情况近似点声源、线声源处理。
2.3.声波的叠加
前面讨论的各类声波都是只包含单个频率的简谐声波。而实际遇到的声场,如谈话声、音乐声、机器运转声等,不只含有一个频率或只有一个声源。这样就涉及到声的叠加原理,各声源所激起的声波可在同一媒质中独立地传播,在各个波的交叠区域,各质点的声振动是各个波在该点激起的更复杂的复合振动。在处理声波的反射问题时也会用到叠加原理。
声波的叠加属于能量的叠加:即按照能量叠加原则进行声波声压的叠加。
声波的能量主要包括了媒质的传递过程中的粒子动能与粒子间相对的势能。
当为瞬时声压时,由于方向矢量的忽略,可视为声压的直接相加,即:
![]()
有效声压的加合:
![]()
当非瞬时声压,需考虑振动方向等时,则必须考虑矢量加和,按照能量加和原则进行加和。(参见声能密度:![]() )
)
![]()
类同于:
能量加和:如声能密度的加和,即从能量角度考虑,合成后总声场的声能密度:
![]()
其中:![]() ,
,![]() (
(![]() 时的特例)
时的特例)
l 不相干声波:
在一般的噪声问题中,经常遇到的多个声波.或者是频率互不相同,或者是相互之间并不存在固定的相位差,或者是两者兼有,也就是说,这些声波是互不相干的。这样对于空间某定点,![]() 不再是固定的常值,而是随时间做无规变化,叠加后的合成声场不会出现驻波现象。
不再是固定的常值,而是随时间做无规变化,叠加后的合成声场不会出现驻波现象。
2.4.声波的反射、透射、折射和衍射
声波在空间传播时会遇到各种障碍物,或者遇到两种媒质的界面。这时,依据障碍物的形状和大小,会产生声波的反射、透射、折射和衍射。声波的这些特点与光波相近。
反射声波:当声波入射到两种媒质的界面时,一部分会经界面反射回原来的媒质中,即为反射声波(P17) 。另一部分会经界面进入另一种媒质中成为透射声波。(P17)
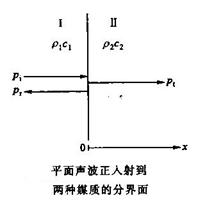

以平面声波为例: 入射声波pi垂直入射到媒质I和媒质Ⅱ的分界面,媒质I的特性阻抗为![]() ,媒质Ⅱ的特性阻抗为
,媒质Ⅱ的特性阻抗为![]() ,分界面位于
,分界面位于![]() 处。
处。
所谓的分界面是相当薄的一层,因此在分界面两边的声压是连续相等的:
![]()
且因为两种媒质在界面密切接触,界面两边媒质质点的法向振动速度也应该连续相等,即: ![]()
将在媒质I中沿正x方向传播的入射平面声波表示为:
![]()
其中 ![]()
当![]() 入射到x=0处的分界面时,在媒质I中产生沿负x方向传播的反射波
入射到x=0处的分界面时,在媒质I中产生沿负x方向传播的反射波![]() ,在媒质Ⅱ中产生沿正x方向传播的透射声波
,在媒质Ⅱ中产生沿正x方向传播的透射声波![]() ,分别表示为:
,分别表示为:
![]()
![]()
其中 ![]()
在媒质I中的声压:
![]()
在媒质Ⅱ中的声压:
![]()
相应的质点振动速度:
在媒质I中的振动速度:![]()
在媒质Ⅱ中的振动速度:![]()
在x=0处, 质点声压和振动速度连续,则有:
 由边界条件式可得下列衡量指标系数.
由边界条件式可得下列衡量指标系数.
专业衡量指标为声压的反射系数![]() 和透射系数
和透射系数![]() :
:
![]()
![]()
专业衡量指标为声强的反射系数![]() 和透射系数
和透射系数![]() :
:

![]()
验证表明![]() 符合能量守恒定律。
符合能量守恒定律。
l 斜入射声波的声学特性:
A.入射声波、反射声波、折射声波满足Snell定律:
![]() 说明声速和方向等时变化的关联性。
说明声速和方向等时变化的关联性。
B.边界条件 截面垂直方向的一致性。
截面垂直方向的一致性。
C吸声系数:入射声波在界面上失去的声能(含透射声能)与入射声能之比。
![]() 说明:斜入射会造成声能损失,即吸声系数与方向相关。
说明:斜入射会造成声能损失,即吸声系数与方向相关。
l 声波的散射与衍射
障碍物的表面粗糙时(主要存在表面起伏与声波波长相当时),或者障碍物的大小与声波波长差不多时,入射声波会向各个方向散射,此时,障碍物周围的声场是由入射声波和散射声波叠加而成。散射声波的图形主要受传递方向与障碍物形状的影响。
当入射声波绕过障碍物传导其背面形成声波的传递,即称为声波的衍射。一般,声波越长,这种现象越明显。声波波长较短时,或声波频率较高(声速一定)时衍射现象较弱。![]()
